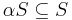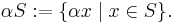Balanced set
In linear algebra and related areas of mathematics a balanced set, circled set or disk in a vector space (over a field K with an absolute value |.|) is a set S so that for all scalars α with |α| ≤ 1
with
The balanced hull or balanced envelope for a set S is the smallest balanced set containing S. It can be constructed as the intersection of all balanced sets containing S.
Contents |
Examples
- The unit ball in a normed vector space is a balanced set.
- Any subspace of a real or complex vector space is a balanced set.
- The cartesian product of a family of balanced sets is balanced in the product space of the corresponding vector spaces (over the same field K).
- Consider C, the field of complex numbers, as a 1-dimensional vector space. The balanced sets are C itself, the empty set and the open and closed discs centered at 0 (visualizing complex numbers as points in the plane). Contrariwise, in the two dimensional Euclidean space there are many more balanced sets: any line segment with midpoint at (0,0) will do. As a result, C and R2 are entirely different as far as their vector space structure is concerned.
- If p is a semi-norm on a linear space X, then for any constant c>0, the set {p≤c} is balanced.
Properties
- The union and intersection of balanced sets is a balanced set.
- The closure of a balanced set is balanced.
- By definition, a set is absolutely convex if and only if it is convex and balanced.
See also
References
- Robertson, A.P.; W.J. Robertson (1964). Topological vector spaces. Cambridge Tracts in Mathematics. 53. Cambridge University Press. p. 4.
- W. Rudin (1990). Functional Analysis (2nd ed ed.). McGraw-Hill, Inc. ISBN 0070542368.
- H.H. Schaefer (1970). Topological Vector Spaces. GTM. 3. Springer-Verlag. p. 11. ISBN 0-387-05380-8.